Median of Medians Algorithm
If one instead consistently chooses "good" pivots, this is avoided and one always gets linear performance even in the worst case. A "good" pivot is one for which we can establish that a constant proportion of elements fall both below and above it, as then the search set decreases at least by a constant proportion at each step, hence exponentially quickly, and the overall time remains linear. The median is a good pivot – the best for sorting, and the best overall choice for selection – decreasing the search set by half at each step. Thus if one can compute the median in linear time, this only adds linear time to each step, and thus the overall complexity of the algorithm remains linear.
The median-of-medians algorithm does not actually compute the exact median, but computes an approximate median, namely a point that is guaranteed to be between the 30th and 70th percentiles . Thus the search set decreases by a fixed proportion at each step, namely at least 30% (so at most 70% left). Lastly, the overhead of computing the pivot consists of recursing in a set of size 20% the size of the original search set, plus a linear factor, so at linear cost at each step, the problem is reduced to 90% (20% and 70%) the original size, which is a fixed proportion smaller, and thus by induction the overall complexity is linear in size.
Median-of-medians algorithm:
- Line up elements in groups of five (this number 5 is not important, it could be e.g. 7 without changing the algorithm much). Call each group S[i], with i ranging from 1 to n/5.
- Find the median of each group. (Call this x[i]). This takes 6 comparisons per group, so 6n/5 total (it is linear time because we are taking medians of very small subsets).
- Find the median of the x[i], using a recursive call to the algorithm. If we write a recurrence in which T(n) is the time to run the algorithm on a list of n items, this step takes time T(n/5). Let M be this median of medians.
- Use M to partition the input and call the algorithm recursively on one of the partitions, just like in quickselect.
| 12 | 15 | 11 | 2 | 9 | 5 | 0 | 7 | 3 | 21 | 44 | 40 | 1 | 18 | 20 | 32 | 19 | 35 | 37 | 39 | ||||||||||||||||||||
| 13 | 16 | 14 | 8 | 10 | 26 | 6 | 33 | 4 | 27 | 49 | 46 | 52 | 25 | 51 | 34 | 43 | 56 | 72 | 79 | ||||||||||||||||||||
| Medians | 17 | 23 | 24 | 28 | 29 | 30 | 31 | 36 | 42 | 47 | 50 | 55 | 58 | 60 | 63 | 65 | 66 | 67 | 81 | 83 | |||||||||||||||||||
| 22 | 45 | 38 | 53 | 61 | 41 | 62 | 82 | 54 | 48 | 59 | 57 | 71 | 78 | 64 | 80 | 70 | 76 | 85 | 87 | ||||||||||||||||||||
| 96 | 95 | 94 | 86 | 89 | 69 | 68 | 97 | 73 | 92 | 74 | 88 | 99 | 84 | 75 | 90 | 77 | 93 | 98 | 91 |
Proof of O(n) running time
The median-calculating recursive call does not exceed worst-case linear behavior because the list of medians is 20% of the size of the list, while the other recursive call recurses on at most 70% of the list, making the running timeFrom this, using induction – or summing the geometric series, obtaining
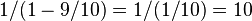 for overall scaling factor – one can easily show that
for overall scaling factor – one can easily show thatCode
// selects the median of medians in an array
int select(int *a, int s, int e, int k){
// if the partition length is less than or equal to 5
// we can sort and find the kth element of it
// this way we can find the median of n/5 partitions
if(e-s+1 <= 5){
sort(a+s, a+e);
return s+k-1;
}
// if array is bigger
// we partition the array in subarrays of size 5
// no. of partitions = n/5 = (e+1)/5
// iterate through each partition
// and recursively calculate the median of all of them
// and keep putting the medians in the starting of the array
for(int i=0; i<(e+1)/5; i++){
int left = 5*i;
int right = left + 4;
if(right > e) right = e;
int median = select(a, 5*i, 5*i+4, 3);
swap(a[median], a[i]);
}
// now we have array
// a[0] = median of 1st 5 sized partition
// a[1] = median of 2nd 5 sized partition
// and so on till n/5
// to find out the median of these n/5 medians
// we need to select the n/10th element of this set (i.e. middle of it)
return select(a, 0, (e+1)/5, (e+1)/10);
}
int main(){
int a[] = {6,7,8,1,2,3,4,5,9,10};
int n = 10;
int mom = select(a, 0, n-1, n/2);
cout<<"Median of Medians: " << a[mom] << endl;
return 0;
}

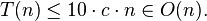
in line:
ReplyDeletereturn select(a, 0, (e+1)/5, (e+1)/10);
If e = 8,
returns -1... bug
citrus fruit,semi-finished bread,margarine,ready soups
ReplyDeletetropical fruit,yogurt,coffee
whole milk
pip fruit,yogurt,cream cheese ,meat spreads
other vegetables,whole milk,condensed milk,long life bakery product
whole milk,butter,yogurt,rice,abrasive cleaner
rolls/buns
other vegetables,UHT-milk,rolls/buns,bottled beer,liquor (appetizer)
pot plants
whole milk,cereals
The code was motivational to build a median of median algorithm. The median can now be used as a partition. However, the code has bugs for values less than 5. Here is the modified version:
ReplyDeleteint select(vector &arr, int s, int e, int k){
if(e-s+1 <= 5){
//If the difference was 1, return s only
int end;
end = e;
end = end + 1;
int diff = end - s;
if(diff == 1)
{
return s;
}
else{
insertionSort(arr, s, e+1);
return s + k;
}
}
// if array is bigger
// we partition the array in subarrays of size 5
// and total number of partitions is ceiling of division by 5
float maxIter = (float(e+1)/5);
maxIter = ceil(maxIter);
//Instead of finding the median from 3rd position, if the difference is even subtract 1
//If the difference is odd divide by 2
for(int i=0; i < maxIter; i++){
cout << endl;
int left = 5*i;
int right = left + 4;
if(right > e){
right = e;
}
int difference = right - left;
difference++;
if(difference%2==0)
{
difference = (difference/2) - 1;
}
else
{
difference = difference/2;
}
int median = select(arr, left, right, difference);
swap(arr[median], arr[i]);
}
selector = (e+1)/10;
return select(arr, 0, maxIter - 1, selector);
}